Merge Sort

LikeQuickSort, Merge Sort is aDivide and Conqueralgorithm. It divides input array in two halves, calls itself for the two halves and then merges the two sorted halves.The merge() functionis used for merging two halves. The merge(arr, l, m, r) is key process that assumes that arr[l..m] and arr[m+1..r] are sorted and merges the two sorted sub-arrays into one. See following C implementation for details.

MergeSort(arr[], l,  r)

If r 
>
 l

1. 
Find the middle point to divide the array into two halves:  
             middle m = (l+r)/2

 2. 
Call mergeSort for first half:   
             Call mergeSort(arr, l, m)

3.
 Call mergeSort for second half:
             Call mergeSort(arr, m+1, r)

4. 
Merge the two halves sorted in step 2 and 3:
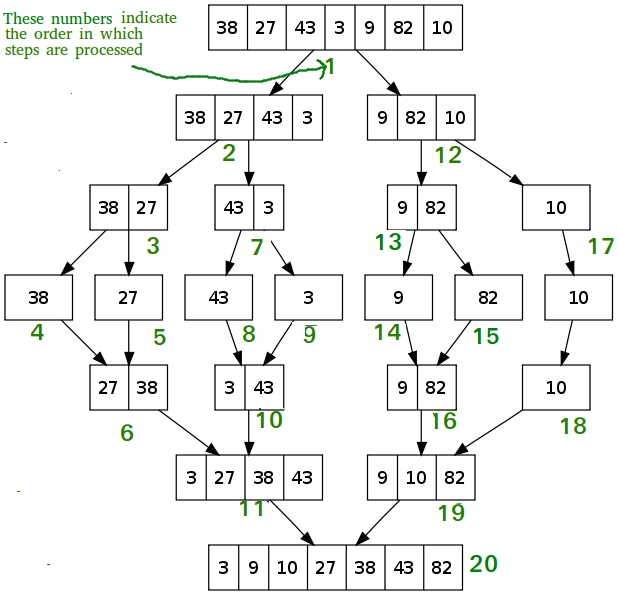
             Call merge(arr, l, m, r)

The following diagram fromwikipediashows the complete merge sort process for an example array {38, 27, 43, 3, 9, 82, 10}. If we take a closer look at the diagram, we can see that the array is recursively divided in two halves till the size becomes 1. Once the size becomes 1, the merge processes comes into action and starts merging arrays back till the complete array is merged.

Merge-Sort-Tutorial

public class Solution {
    /**
     * @param A an integer array
     * @return void
     */
    public void sortIntegers2(int[] A) {
        // use a shared temp array, the extra memory is O(n) at least
        int[] temp = new int[A.length];
        mergeSort(A, 0, A.length - 1, temp);
    }

    private void mergeSort(int[] A, int start, int end, int[] temp) {
        if (start >= end) {
            return;
        }

        int left = start, right = end;
        int mid = (start + end) / 2;

        mergeSort(A, start, mid, temp);
        mergeSort(A, mid+1, end, temp);
        merge(A, start, mid, end, temp);
    }

    private void merge(int[] A, int start, int mid, int end, int[] temp) {
        int left = start;
        int right = mid+1;
        int index = start;

        // merge two sorted subarrays in A to temp array
        while (left <= mid && right <= end) {
            if (A[left] < A[right]) {
                temp[index++] = A[left++];
            } else {
                temp[index++] = A[right++];
            }
        }
        while (left <= mid) {
            temp[index++] = A[left++];
        }
        while (right <= end) {
            temp[index++] = A[right++];
        }

        // copy temp back to A
        for (index = start; index <= end; index++) {
            A[index] = temp[index];
        }
    }
}