Quick Sort

快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)。

https://www.zybuluo.com/Zh1Cheung/note/1076005

核心思想就是，找到pivot 然后用这个pivot作为base , 通过双指针的方法，左右移动到pivot，确保，左边的数值全部小于pivot ,右面的数值全部大于pivot,然后再通过divide conquer 进行左右两部分的后续操作，直到不能拆分pivot为止。

代码小技巧：左指针移动比较完成后，一定要落回P点,如果数据都是小于p的。所以合理处理 =

难点： 你的第一次while循环之后，并不能保证此时所有小于分割处的数字在它的左边，大于的在它数在它的右边。

如果只有两个数值的时候，就回出现，left = p 在同一点。

while (left <= right && A[left] < pivot) 循环滑动技巧


https://zhuanlan.zhihu.com/p/34479151

时间复杂度：

在最优情况下，Partition每次都划分得很均匀，如果排序n个关键字，其递归树的深度就为.log2n.+1（.x.表示不大于x的最大整数），即仅需递归log2n次，需要时间为T（n）的话，第一次Partiation应该是需要对整个数组扫描一遍，做n次比较。然后，获得的枢轴将数组一分为二，那么各自还需要T（n/2）的时间（注意是最好情况，所以平分两半）。于是不断地划分下去，我们就有了下面的不等式推断。

1. T（n）≤2T（n/2） +n，T（1）=0

2. T（n）≤2（2T（n/4）+n/2） +

   n

   =

   4T

   （n/4）+2n

3. T（n）≤4（2T（n/8）+n/4） +

   2n

   =

   8T

   （n/8）+3n

4. ……

5. T（n）≤nT（1）+（log2n）×

   n

   =

   O

   (nlogn)

也就是说，在最优的情况下，快速排序算法的时间复杂度为O(nlogn)。

在最坏的情况下，待排序的序列为正序或者逆序，每次划分只得到一个比上一次划分少一个记录的子序列，注意另一个为空。如果递归树画出来，它就是一棵斜树。此时需要执行n‐1次递归调用，且第i次划分需要经过n‐i次关键字的比较才能找到第i个记录，也就是枢轴的位置，因此比较次数为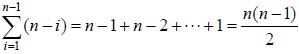 ，最终其时间复杂度为O(n2)。

平均的情况，设枢轴的关键字应该在第k的位置（1≤k≤n），那么：

public class Solution {
    /**
     * @param A an integer array
     * @return void
     */
    public void sortIntegers2(int[] A) {
        quickSort(A, 0, A.length - 1);
    }

    private void quickSort(int[] A, int start, int end)
        {
            if (start >= end)
            {
                return;
            }

            int left = start, right = end;
            // key point 1: pivot is the value, not the index
            int pivot = A[(start + end) / 2];

            while (left <= right)
            {
                while (A[left] < pivot)
                {
                    left++;
                }
                while (A[right] > pivot)
                {
                    right--;
                }

                if (left <= right)
                {
                    int temp = A[left];
                    A[left] = A[right];
                    A[right] = temp;

                    left++;
                    right--;
                }
            }

            quickSort(A, start, right);
            quickSort(A, left, end);
        }
}